1. 그래프
자료구조에는 선형 자료구조(배열, 리스트, 스택, 큐 등)와 비선형 자료구조(그래프, 트리 등)이 있습니다.
선형 자료구조는 데이터의 순서가 중요한 자료구조입니다.
반면 비선형 자료구조는 데이터의 관계를 표현한 자료구조입니다.
그래프는 노드와 간선으로 표현할 수 있습니다.
노드는 데이터 자체를 의미하고, 간선은 관계를 의미합니다.
간선은 단방향과 양방향으로 또 나뉩니다.
단방향은 한 노드에서 다른 한 노드로만 향하는 관계일 때 사용되며, 양방향은 양 노드가 서로를 향하는 관계일 때 사용됩니다.
이때 양방향은 방향성을 반드시 표현하지 않아도 됩니다.
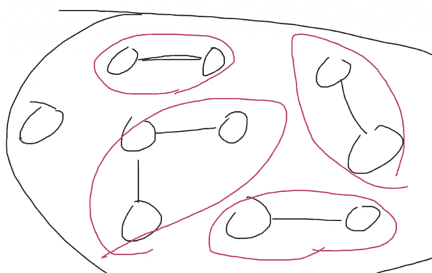
그래프에서 '연결 요소' 라는 단어가 있습니다.
연결 요소는 연결된 노드를 하나의 집합으로 묶어서 부르는 것을 의미합니다.
예를 들어 아래 그림의 경우 연결 요소는 5개입니다.
'가중치' 라는 단어도 있습니다.
한 노드에서 다른 노드로 향할 때, 간선의 크기를 의미합니다.
예를 들어, 서울이 노드 A, 부산이 노드 B라고 할 때, A에서 B로 향하는 가중치는 10이라고 표현할 수 있습니다.
2. 그래프 탐색 알고리즘
그래프를 탐색하는 방법(알고리즘)에는 크게 두 가지가 있습니다. DFS와 BFS 입니다.
2.1. DFS (Depth First Search)
2.1.1. 특징
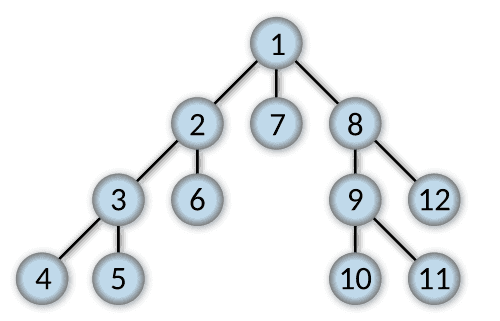
깊이 우선 탐색이라 불리는 DFS는, 그래프를 탐색할 때 다음 노드를 먼저 방문하는 식으로 탐색합니다.
이미지로 표현하면 다음과 같습니다.
2.1.2. 용도
DFS를 주로 사용하는 경우는 다음과 같습니다.
- 연결 요소의 크기 구하기
- 연결 요소의 개수 구하기
- Flood Fill
- 2차원 배열의 데이터가 주어지고, 특정 위치의 연결 요소의 크기를 구하는 경우가 있을 때, 이 크기를 DFS를 이용하여 구할 수 있습니다. (대표적인 문제)
- 이분 그래프 판별
- 사이클 존재 파악 및 사이클 크기 구하기
2.1.3. 기본 구현
DFS를 구현할 때 가장 먼저, 주어진 노드와 간선 정보를 그래프 형태로 저장해야 합니다.
그래프를 저장할 때는 인접 행렬과 인접 그래프 방식으로 구현할 수 있습니다.
- 인접 행렬
2차원 배열을 만들고, 연결 정보를 이 배열에 저장합니다.
만약 arr 라는 이름의 변수가 있다고 가정하면 노드 x에서 노드 y로 향하는 간선의 정보는 arr[x][y]로 접근할 수 있습니다.
간선의 개수가 k개이고, 모든 간선의 가중치가 1인 양방향 그래프인 경우 아래 코드와 같이 저장할 수 있습니다.
arr = [[0] * n for _ in range(n)]
for _ in range(k): # k: 간선의 개수
a, b = map(int, input().split())
arr[a][b] = 1
arr[b][a] = 0- 인접 그래프
각 노드에 연결된 노드를 리스트 형태로 저장합니다.
만약 n개의 노드와 k개의 간선이 있다고 가정하면, 인접 그래프로 저장하는 코드는 다음과 같습니다.
graph = [[] * for _ in range(n)]
for _ in range(k): # k: 간선의 개수
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)인접 행렬은 공간을 더 많이 차지하는 대신, O(1) 만에 연결 정보를 조회할 수 있는 장점이 있습니다.
반면, 인접 그래프는 공간을 더 효울적으로 사용하는 대신, 그래프를 탐색할 때 연결된 노드 개수만큼 선형적으로 늘어난다는 단점이 있습니다.
따라서 문제 요구사항이나 제약 조건에 따라 적절한 방식을 사용하는 것이 좋겠습니다.
이제 DFS 탐색을 위해서는 다음과 같이 작성할 수 있는데요. 인접 그래프 형태로 저장했다고 가정하고 구현해보겠습니다.
이때 한 노드를 중복 방문하는 것을 방지하기 위해 visited = [False] * n 과 같이 배열 형태로 값을 기록하는데요. 방문 처리는 DFS 함수 내부의 첫 번째 라인에서 수행하는 것이 권장됩니다.
특정 노드에 방문했을 때 해야 할 일(방문 표시, 결과 합산 등)이 한곳에 모여 있어 코드가 깔끔하고 별도로 처리해줄 필요가 없어 실수할 확률이 줄어듭니다. 또한 재귀 함수는 자기 자신을 정의하는 함수라는 측면에서도 자연스럽습니다.
# 파이썬의 기본 재귀 호출 한도는 보통 1,000회로 제한됩니다.
# 따라서 `sys` 모듈의 `setrecursionlimit=n`으로 최대 한도를 설정합니다.
import sys
sys.setrecursionlimit(n**2)
# 그래프
graph = [[] * for _ in range(n)]
for _ in range(k): # k: 간선의 개수
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
# 노드 방문 여부
visited = [False] * n
# DFS 로직
def dfs(curr_node):
visited[curr_node] = True
for next_node in graph[curr_node]:
if visited[next_node]:
continue
dfs(next_node)위 DFS 코드를 기반으로, 문제에서 필요한 해를 구하는 코드를 추가하면 됩니다.
2.1.4. 이분 그래프
이분 그래프란, 모든 정점을 빨간색, 혹은 파란색으로 칠했을 때, 모든 간선에 대해서 각 간선이 빨간색이랑 파란색을 포함하도록 색칠할 수 있는 그래프입니다.
이분 그래프도 DFS 알고리즘을 이용해서 판별할 수 있습니다.
import sys
# 이분 그래프 판별 함수
def is_bipartite_graph(curr, color):
colors[curr] = color
for nxt in graph[curr]:
if colors[nxt] != 0: # 이미 방문을 한 적이 있는 노드
if color[nxt] == color[curr]: # 연결된 노드와 현재 노드의 색상이 같으면 이분 그래프가 아니게 된다.
answer = False
return False
continue
# 연결된 노드를 탐색하면서 현재 노드와 다른 색상으로 칠한다.
if not is_bipartite_graph(nxt, colors[curr] * -1):
return False
return True
n, m = map(int, input().split())
sys.setrecursionlimit(n**2)
# 그래프 생성
graph = [[] for _ in range(n + 1)]
for _ in range(m):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
colors = [0] * (n + 1) # 색상 기록 배열. 0: 방문하지 않은 노드, 1: 빨간색, -1: 파란색
answer = True
for i in range(1, n + 1):
if colors[i] == 0: # 아직 방문하지 않았다면
if not is_bipartite_graph(i, 1):
answer = False
break
print(answer)2.1.5. 사이클 존재 유무 파악 및 사이클 크기 구하기
그래프에 사이클이 존재하는지 판별할 수 있고, 사이클의 크기도 DFS를 통해 구할 수 있습니다.
기본 구현(Python)은 다음과 같습니다.
depth = [0] * n # 각 노드의 방문 깊이(순서)를 기록하는 배열입니다.
has_cycle = False
# cur: 현재 방문한 노드 번호입니다.
# prev: 이전에 방문한 노드 번호입니다.
def dfs(curr, prev):
for nxt in graph[curr]:
if prev != nxt: # curr과 연결된 노드인 경우
if depth[nxt] == 0: # 해당 노드에 처음 방문하는 경우
depth[nxt] = depth[curr] + 1
dfs(nxt, curr)
elif depth[nxt] > depth[curr]: # 연결된 노드가 현재 노드보다 먼저 방문한 경우 -> 사이클 존재
has_cycle = True
size = depth[curr] - depth[nxt] + 1 # 사이클의 사이즈를 구한다. 대표적인 문제로는 백준의 아침은 고구마야가 있으니 위를 참고하여 풀어보는 것도 좋겠습니다.
2.2. BFS
2.2.1. 특징
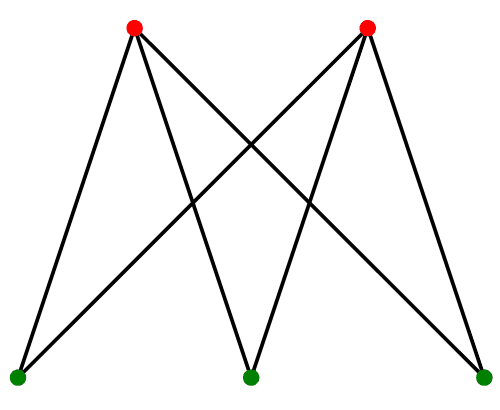
너비 우선 탐색이라 불리는 BFS(Breadth First Search)는 그래프 상에서 특정 노드를 기준으로, 연결된 노드를 먼저 탐색하는 방식입니다.
말보단 아래 이미지를 보는 것이 이해가 훨씬 쉽습니다.
2.2.2. 용도
- 가중치가 모두 1인 그래프에서 최단 거리 구하기 ()
- 단계별 확산 시뮬레이션
- 그래프에서 depth 단위로 끊어서 탐색하기
2.2.3. 기본 구현
DFS는 재귀 함수로 구현하는 반면, BFS는 큐를 이용해서 구현합니다.
인접 그래프 형태의 자료구조에서는 다음과 같이 작성하는 것이 기본 형태입니다.
from collections import deque
def bfs(start):
visited = [False] * n
q = deque()
visited[start] = True
q.append(start)
while q:
curr = q.popleft()
for next in graph[curr]:
if visited[next]:
continue
q.append(next)
visited[next] = True이때 유의해야 할 점은, 방문 여부를 처리할 때 반드시 큐에 넣기 전에 해야 한다는 점입니다.
큐에서 뺄 때 처리하면, 중복된 노드가 큐에 여러 번 들어갈 수 있어 불필요한 연산이 수행될 수 있기 때문입니다.
만약 2차원 격자에서 BFS 방식으로 탐색하려면 다음과 같이 작성하는 것이 기본 형태입니다.
from collections import deque
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
def bfs(start_x, start_y):
visited = [[False] * n for _ in range(n)]
q = deque((start_x, start_y))
visited[start_x][start_y] = True
q.append((start_x, start_y))
while q:
x, y = q.popleft()
for d in range(4):
next_x, next_y = x + dx[d], y + dy[d]
if not in_array(next_x, next_y):
continue
if visited[next_x][next_y]:
continue
visited[next_x][next_y] = True
q.append((next_x, next_y))2.2.4. 그래프에서 depth 단위로 끊어서 탐색하기
from collections import deque
graph = ... # 생략
visited = [False] * n
q = deque()
q.append(n)
visited[n] = True
# while문이 실행될 때마다 시작 노드(n)를 기준으로 거리가 1씩 증가하는 노드들만 탐색하게 된다.
# (거리가 1인 노드들 -> 거리가 2인 노드들 -> ...)
while q:
size = len(q)
for _ in range(size):
curr = q.popleft()
for nxt in graph[curr]:
if visited[nxt]:
continue
q.append(nxt)
visited[nxt] = True